优先级队列是常用的数据结构,区别于 FIFO 先进先出队列,优先级队列中的元素都具有优先级关系,出队时需要按照优先级顺序出队。元素的优先级是自定义的,可以按照时间、大小等。
这里还有一个问题,为什么我们需要优先级队列,我们直接把所有元素都排序不就好了吗,按照排序后的顺序进行出队。这么说也没错,但有些场景还是用优先级队列比较合适,比如说我们不需要处理所有的元素。假设我们有 n 个元素(n 非常大),需要找出最大的 k 个,如果用快速排序全排序,时间复杂度是 O(nlogn);如果使用优先级队列,时间复杂度是O(nlogk),在这种解决问题的思路中需要先构建一个大小为 k 的优先级队列,假设我们用堆来实现,这个建堆的复杂度为 O(logk),找最大值,需要使用最小堆,(因为我们最终要保证最小堆的所有 k 个元素都比剩下的 n-k 大,那我们只要保证 k 个元素的最小值比剩下的 n-k 个大就可以了,所以要用最小堆),建完堆之后,要比较剩下的 n-k 个元素跟堆顶元素的大小,如果比堆顶大,则要替换堆顶的元素。所以总的时间复杂度是 O(nlogk)。
数据结构-堆
对可以用来实现优先级队列,我们首先看下堆这个数据结构,以最小堆为例,它的特点为:
- 堆是一颗完全二叉树:什么是完全二叉树?树的所有层中,除了最后一层,其他层都是满的。最大堆和最小堆都是完全二叉树。
- 最小堆中,堆顶元素比左右两个子树的元素都小,这个定义是递归的,适用于两个子树。(这个需要额外注意,堆只是定义了树中 parent 以及 children 的大小关系,纵向大小关系,底层数组并不是全局有序的)
下图是一个最小堆的示例
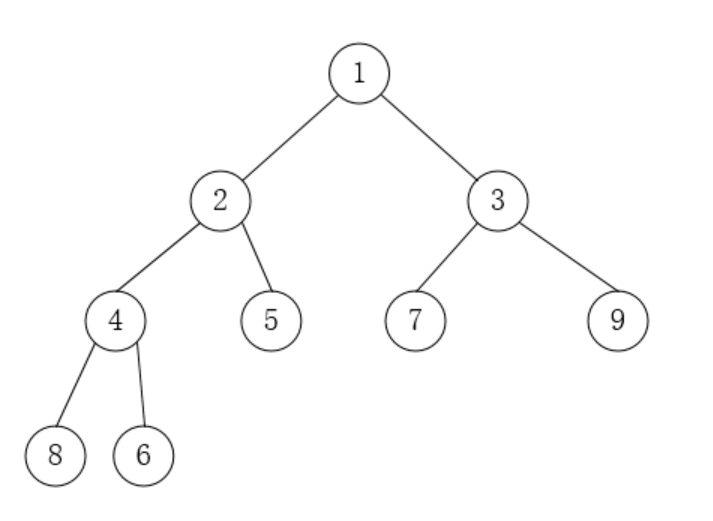
堆的主要操作跟普通队列类似,即 Push 和 Pop:
- Push,向堆中添加一个元素,添加的元素可能会影响堆的性质,破坏了堆的结构,所以需要一些调整操作。
- Pop,移除堆顶操作,把堆顶移除了,堆顶就没有元素了,这个时候需要把堆的最后一个元素放到堆顶,然后重新调整为堆。(为什么要把最后一个元素放到堆顶呢?因为要保持完全二叉树的结构)
为了建堆以及堆结构变化之后进行调整,堆有两个常见的内部操作(这里用小写的 down 和 up 表示以示为内部操作):
- down(i, n):向下调整,调整下标 i,n 为数组长度,以最小堆为例,向下调整的方法为:假设当前要调整的下标为 i,看 i 的左孩子和右孩子,将 i 和左孩子和右孩子的较小者进行交换(如果 i 比两个孩子都小,那就不需要交换了),向下调整时, i 下标之前的元素是不会被调整的。同时因为交换了 i 和孩子,孩子也需要向下调整。
- up(i):向上调整,将下标 i 向上调整,向上调整比向下调整简单,先找到 i 的 parent,如果比 parent 大,则交换,同时也要看下 parent 需不需要调整,这个过程一直持续到堆顶。
有了 down 和 up 操作,建堆、Push、Pop 的实现就相对清晰一些了,其中
- 建堆: 从最后一个非叶节点(n/2-1)开始执行 down 操作,直到第一个节点,(额外说明一下,建堆的时间复杂度是
O(n)) - Push: 将元素添加到最后一个节点,然后执行 up 操作
- Pop: 取出堆顶元素,将最后一个元素调到堆顶,然后将堆顶元素执行 down 操作,只需要调整堆顶元素就可以了,其他元素结构都是正常的。
Golang 中堆的实现
Golang 中有一个堆的实现,我们可以直接拿来用(自己实现堆比较容易出错,建议用好已有的sdk就可以了),在 Go 中,给出的是一个接口,需要自己实现相关方法,接口定义如下:
// heap.Interface
type Interface interface {
sort.Interface
// 这里需要注意,这两个接口的参数和返回值为 interface{} 用的时候,需要进行强制类型转换
Push(x interface{}) // add x as element Len()
Pop() interface{} // remove and return element Len() - 1.
}
// sort.Interface
type Interface interface {
Len() int
Less(i, j int) bool
Swap(i, j int)
}
其中 sort.Interface 是用来比较元素大小的,我们 Golang 中排序的经常用到这个接口,heap.Interface 额外添加了两个接口 Push 和 Pop,这两个接口的定义十分别扭,首先,这两个接口不是给我们使用的,是 heap 内部自己为了调整堆结构使用的,其次这两个接口跟我们在上一小节提到的 Push 和 Pop 功能不一样,其中 Push 是追加到数组的末尾(仅此而已,不需要调整),Pop 是返回数组的最后一个元素,并且删除这最后一个元素(仅此而已,也不是什么堆顶元素)。Go 额外提供了全局的 heap.Pop(h Interface) interface{} 和 heap.Push(h Interface, x interface{}) 方法供我们使用。除了这两个方法,还有一个 heap.Init(h Interface) 用来建堆。
golang 官方提供了一个示例,通过这个示例,我们看下接口的实现和使用。
import (
"container/heap"
"fmt"
)
// 此示例是一个最小堆的实现
type IntHeap []int
func (h IntHeap) Len() int { return len(h) }
// 注意这个 Less 方法决定了是要构建最大堆还是最小堆
func (h IntHeap) Less(i, j int) bool { return h[i] < h[j] }
func (h IntHeap) Swap(i, j int) { h[i], h[j] = h[j], h[i] }
// 因为要修改 slice 的结构,所以要使用 pointer receivers
// 直接将元素放到最后一个位置
func (h *IntHeap) Push(x interface{}) {
*h = append(*h, x.(int))
}
// 返回最后一个元素,并将这个元素从 slice 中删除
func (h *IntHeap) Pop() interface{} {
old := *h
n := len(old)
x := old[n-1]
*h = old[0 : n-1]
return x
}
func Example_intHeap() {
// IntHeap 实现了 heap.Interface 接口
h := &IntHeap{2, 1, 5}
// heap.Init 用来建堆
heap.Init(h)
// heap.Push 额外添加一个元素,并进行调整
heap.Push(h, 3)
// 最小的元素在堆顶
fmt.Printf("minimum: %d\n", (*h)[0])
// heap.Pop 取出堆顶的最小元素,并重新建堆
for h.Len() > 0 {
fmt.Printf("%d ", heap.Pop(h))
}
// Output:
// minimum: 1
// 1 2 3 5
}
优先级队列使用:数组中最大的 K 个数
取出一个数组中,最大的 k 个数,我们可以先使用 k 个数,构建一个大小为 k 的最小堆,然后把剩下的元素同堆顶元素比较,如果比最小值大,就把最小的值pop出来,把当前值放进去。这样结束之后,这个大小为 k 的堆就是最大的 k 个数。代码如下。
// int[0] is min value
type MinHeap []int
func (minHeap MinHeap) Len() int { return len(minHeap) }
// 小的放在前面就是最小堆
func (minHeap MinHeap) Less(i, j int) bool { return minHeap[i] < minHeap[j] }
func (minHeap MinHeap) Swap(i, j int) {
minHeap[i], minHeap[j] = minHeap[j], minHeap[i]
}
func (minHeap *MinHeap) Pop() interface{} {
x := (*minHeap)[len(*minHeap)-1]
*minHeap = (*minHeap)[0 : len(*minHeap)-1]
return x
}
func (minHeap *MinHeap) Push(e interface{}) {
*minHeap = append(*minHeap, e.(int))
}
func main() {
fmt.Println(findMaxKElement([]int{121, 14, 46, 9, 5, 10}, 3))
}
func findMaxKElement(a []int, k int) []int {
mh := make([]int,0)
mHeap := &MinHeap(mh)
for i := 0; i < k; i++ {
heap.Push(mHeap, a[i])
}
for i := k; i < len(a); i++ {
if a[i] > mHeap[0] {
heap.Pop(mHeap)
heap.Push(mHeap, a[i])
}
}
return mHeap
}